-
 Symmetric algorithm
Symmetric algorithm
-
 Abortion
Abortion
-
 Apricot
Apricot
-
 Peristalsis
Peristalsis
-
 Critical pressure
Critical pressure
-
 Top plate
Top plate
-
 Retified wood
Retified wood
-
 Venous thrombosis
Venous thrombosis
-
 OCO
OCO
-
 Tulip tree
Tulip tree
-
 Kilobar
Kilobar
-
 Brood
Brood
-
 Inclusion
Inclusion
-
 Potato
Potato
-
 Polysaccharide
Polysaccharide
-
 Neurotrope
Neurotrope
-
 Conventional cytotoxic medicine
Conventional cytotoxic medicine
-
 Sign
Sign
-
 Monophyletic
Monophyletic
-
 Absorption spectrometry
Absorption spectrometry
-
 Myelomeningocoele
Myelomeningocoele
-
 Retractile
Retractile
-
 Air braking
Air braking
-
 Rowan
Rowan
-
 Archipelago
Archipelago
-
 Epstein-Barr virus
Epstein-Barr virus
-
 Microbiome
Microbiome
-
 Hot-tub
Hot-tub
-
 Wetland
Wetland
-
 Friction
Friction
Lagrangian point
A Lagrangian point is a position in space in a two-body system where the gravitational fields combine to form an equilibrium point with a third body of negligible mass, such that the relative positions of the three bodies are fixed.
Lagrangian points are a special case of the 3-body problem where one of the 3 bodies is of negligible mass compared with the other 2.
Sun-Earth application
The Lagrangian points are the points where a body attracted by the Sun and the Earth follows an orbit around the Sun at the same angular velocity as the Earth, under the combined forces of attraction of the Sun and the Earth. Points L1 and L2 are close to the Earth (to a first order, the ratio of the distances is proportional to the cube root of the mass ratios), point L3 is symmetric about the Earth relative to the Sun, and points L4 and L5 are at the vertices of equilateral triangles with the Sun-Earth line as base. Despite what the figure may suggest, where the equipotentials in the rotating reference frame are plotted, the orbits around L4 and L5 are stable, and the other three unstable because of the Coriolis force.
Other examples
The solar probe SOHO: to observe the Sun continuously, point L1 is ideal. It revolves around the Sun with the Earth, with the Sun permanently on one side and the Earth on the opposite side. It was therefore at L1 that the SOHO probe, dedicated to observing the Sun, was placed.
The Planck mission: if, on the other hand, the outer universe is to be observed, as in the Planck project, point L2 is ideal. It revolves around the Earth with the Sun and the Earth permanently opposed to the desired direction. So Planck was placed at L2, as too will be the new space telescope, JWST, Hubble's successor.
The Trojan asteroids: the Trojan asteroids are in the same orbit as Jupiter, either leading Jupiter (point L4) or trailing (point L5).
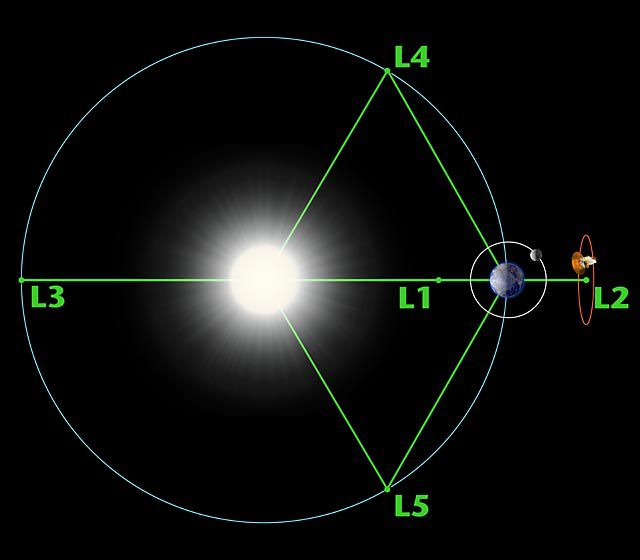 The 5 Lagrangian points, extrema of gravitational potential in a 2-body system. Credit: NASA-WMAP Science Team.
The 5 Lagrangian points, extrema of gravitational potential in a 2-body system. Credit: NASA-WMAP Science Team.
Latest
Fill out my online form.



