-
 Interactive
Interactive
-
 Ares V
Ares V
-
 Camouflage feathers
Camouflage feathers
-
 Erg
Erg
-
 Apple scab
Apple scab
-
 Magnaporthe grisea
Magnaporthe grisea
-
 Comet
Comet
-
 Malpighian tubule
Malpighian tubule
-
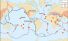 Ridge
Ridge
-
 Eisenmenger complex
Eisenmenger complex
-
 Cotylopus acutipinnis
Cotylopus acutipinnis
-
 Centromere
Centromere
-
 Dehiscence
Dehiscence
-
 Retrotransposon
Retrotransposon
-
 Protostome
Protostome
-
 Nintendo Revolution
Nintendo Revolution
-
 Metamorphosis
Metamorphosis
-
 Balmer formula
Balmer formula
-
 Mixotrophy
Mixotrophy
-
 Glycaemia
Glycaemia
-
 Clinical history
Clinical history
-
 Listeriosis
Listeriosis
-
 Cytoplasm
Cytoplasm
-
 Discovery
Discovery
-
 Ion engine
Ion engine
-
 International Space Station
International Space Station
-
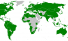 Marpol Convention
Marpol Convention
-
 Glial cells
Glial cells
-
 Lahar
Lahar
-
 Asian brown cloud
Asian brown cloud
Third law of thermodynamics
The third law of thermodynamics, called Nernst's theorem, from the name of the 1906 Nobel prize winner, is stated as follows: "The entropy of any system can always be assumed to be zero at a temperature of absolute zero".
Strictly speaking, this statement only applies to macroscopic bodies and there are some subtleties where degenerate quantum systems are concerned. In practice, no physical systems, even degenerate, are known to violate this law, even though they may be conceivable in quantum mechanical statistics.
At first this theorem was only applied to condensed systems such as liquids and solids, but it has now been generalised to include gaseous systems.
To understand its origins consider the following relationships verified by free energy F and its variations:
From this we have
Nernst set the following stronger condition:
Which gives, for variations of free energy F and the Gibbs function G:
In both cases we obtain the variations in entropy of a system when the temperature tends to absolute zero:
This was the result initially established by Nernst, but Planck went further. He showed that this condition implied that the entropy of all substances tends towards a universal constant when approaching absolute zero.
If this universal constant is given the value 0, the third law of thermodynamics ensues.
This has important consequences, because if we take the molar heat capacity at constant pressure (volume) Cp for one mole of a substance, it should satisfy the following relationship which can give rise to problems as T approaches absolute zero.
The only way of avoiding infinite divergences is then to let
and we then run up against a contradiction of the Dulong and Petit law for which, in a crystalline system obtained by the condensation of a gas for example, the heat capacity must be a constant equal to 3R where R is the ideal gas constant.
The Dulong and Petit law actually no longer holds at low temperatures, but in classical statistical thermodynamics it should do so.
Einstein solved this contradiction by introducing quantum theory. For the scientific community of the time this was the first convincing result in favour of Planck's quanta theory.
Latest
Fill out my online form.



