-
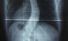 Scoliosis
Scoliosis
-
 Google Earth
Google Earth
-
 EPR reactor
EPR reactor
-
 Joist
Joist
-
 Bile acid chelator
Bile acid chelator
-
 Carbon footprint
Carbon footprint
-
 Subspecies
Subspecies
-
 ISRO
ISRO
-
 Histology
Histology
-
 Reducing agent
Reducing agent
-
 Giant planet
Giant planet
-
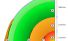 Moho
Moho
-
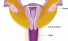 Cervix
Cervix
-
 Etna
Etna
-
 Piscivore
Piscivore
-
 Isostasy
Isostasy
-
 Full hybrid
Full hybrid
-
 Glycerol
Glycerol
-
 Polytypism
Polytypism
-
 Jet Propulsion Laboratory
Jet Propulsion Laboratory
-
 Secondary
Secondary
-
 Proliferation
Proliferation
-
 Hypoxia
Hypoxia
-
 Cadherin
Cadherin
-
 Pterophile
Pterophile
-
 Forums
Forums
-
 Bubonic plague
Bubonic plague
-
 Phycocyanin
Phycocyanin
-
 Information
Information
-
 Starch
Starch
Quantum entanglement
Quantum entanglement is a fundamental phenomenon in quantum mechanics discovered by Einstein and Schrödinger in the 1930s. Two physical systems, such as two particles, are found to be in a quantum state in which they form a single system in a certain subtle way.
Any measurements on one of the systems will affect the other irrespective of the distance between them. Before entanglement, two non-interacting physical systems are in independent quantum states, but after entanglement these two states are in a way "entangled" and it is no longer possible to describe them independently.
This is why, as indicated above, non-local properties appear and a measurement on one system instantly influences the other system, even at a distance of light-years. The entanglement phenomenon is one of the most disturbing in quantum mechanics and is the basis of its Copenhagen interpretation
.
Quantum entanglement is at the heart of the famous experiments known as the EPR paradox and Schrödinger's cat or Wigner's friend. The entanglement phenomenon is based on the mathematical and physical principles of quantum mechanics. That is to say the notions of state vectors and tensor products of these state vectors on the one hand, and the principles of superposition of states and reduction of the state vector on the other hand.
Remember that in quantum mechanics, which is the extension of Heisenberg's matrix mechanics and Schrödinger's wave mechanics, there is a complete reworking of the kinematics and dynamics of the physical and mathematical quantities associated with observable phenomena and physical systems.
Quantum mechanics, even though it deals with wave-particle duality, is not a theory that can be reduced to particle wave mechanics.
The dual nature of matter and light shown in the case of charged particle theory and electromagnetic radiation theory is only a consequence of the reworking of the differential and integral laws associated with physical phenomena and a physical system.
The introduction of the concept of wave function for a particle is then only a very special case of the introduction of the concept of state vector for a physical system with dynamic variables giving rise to a measurable phenomenon, whatever this system and these variables, as long as a notion of energy and interaction between this system and a classical measuring instrument exists.
It is because the differential and integral laws describing the change in space and time of an observable quantity in classical physics naturally have the form of the kinematic laws of a discrete or continuous set of material points, that correspondences are found between the general quantum formulation of these laws and the quantum laws of electrons and photons.
It is important to remember that in classical physics already a phenomenon is measured and defined from the modification in the kinematic and dynamic state of a particle of the material being tested.
An electromagnetic field is defined by its effect on a charged test particle of matter at a point in space and therefore, in particular, a field of light waves.
Temperature can also be defined by the dilation of a material body at one point, and here too, an observable quantity is, in the last analysis, defined by the kinematics of a material point and the sum total of the energy and momentum exchanges.
The solution to the wave-particle duality problem therefore lies in the two central ideas in the Copenhagen interpretation and quantum mechanics in the form given by Dirac, Von Neumann and Weyl from the work of Bohr, Heisenberg and Born.
-in nature there is fundamentally neither wave nor corpuscle in the classical sense. These concepts are only useful and are still used in the theory because they must necessarily establish a correspondence between the form of the quantum laws and the form of classical laws that must emerge from the former.
Just as a test particle serves to define an electromagnetic field, a classical measuring instrument serves to define a quantum system by the way in which this quantum system will affect the measuring instrument. Inevitably, the kinematic and dynamic description of this instrument will involve the classical wave and particle concepts.
Quantum formalism must therefore express both all of this and the fundamental non-existence of the classical particle and wave, just as relativity is based on the non-existence of absolute space and time. This property of formalism is largely satisfied by the Heisenberg inequalities.
-the wave-corpuscle duality is not derived from any subtle association of particles and waves, i.e. there are no special laws restricted to the laws of motion and the structure of particles of matter and to the waves of interaction fields (electromagnetic, nuclear etc.), but there are laws of change in time and space of any physical quantity which are modified, and in particular the general form of a differential law and an integral law.
It is because this framework is quantified that it necessarily applies to any physical system at all. It is very important to remember in this connection that the existence of an energy is an essential property in all the laws of physics. The universality of energy and the fact that any definition of the measurement of a phenomenon is based, in the final analysis, on an interaction with energy automatically ensures that the laws of quantum mechanics apply when describing the change in any arbitrary system.
This is why wave mechanics, which finally is based largely on the existence noted by de Broglie of a strong analogy between Maupertuis' principle for the motion of a particle of matter and Fermat's principle for a light beam, is merely a very special case of quantum mechanics since the latter does not finally apply to the laws governing the motion of particles in space and time but to the change in all directly or indirectly measurable physical quantities.
In particular, the laws of quantum mechanics naturally contain the possibility of creating or destroying a particle and of its transformation into another particle, which is not a phenomenon that can be described using the Fermat or Maupertuis principles.
The construction and form of quantum theory are thus based on the ideas that:
-the laws of physics do not fundamentally apply to something in space and time.
-particles and waves are not fundamental structures but approximations of the form of the laws and objects of the physical world.
-energy is at the heart of the quantification process and ensures/explains the universal character of quantification (the quantification of certain classical dynamic variables, probability amplitudes for observing these values).
However, the laws of quantum mechanics emerged historically and can be introduced for teaching purposes as a first approximation with the wave and matrix mechanics of particles in classical space and time. But it is central to understand as quickly as possible that these mechanics are not the true structure of quantum mechanics.
The way we proceed is reminiscent of thermodynamics which functions independently of whether or not the physical system has any atomic structure. The total energy of the system, called an equation of state of the system, is considered and there is a set of fundamental variables called variables of state related by the energy function and other equations of state of the thermodynamic system. The system is defined as a black box (what is inside is not important) and only the sum totals of input and output energy and the values of the variables of state are measured.
Nevertheless, quantum mechanics does achieve a synthesis of the wave and corpuscular structure for the change of physical values. In particular, this means that the physics and mathematics of waves and fields must appear in the form of these laws such that, when they are applied to particular systems such as classical electrons, protons and electromagnetic fields, we find the wave mechanics of these systems.
Thus the principle of the superposition of fields in electrodynamics and optics must reappear to describe the state of a quantum system. The entire structure of Fourier analysis must especially be present.
Similarly, the structure of analytical mechanics with the Hamiltonian function of the energy of a classical mechanical system must be kept and play a central role.
Bearing in mind the above considerations, the way in which quantum mechanics is constructed starts to become clear.
The observable variables Ai and a total energy H called the Hamiltonian are associated with a physical system.
In the case of a particle having momentum variables Pi and position variables Qi placed in a potential V(Qi), the function H of the particle is written:
H=T(Pi)+V(Qi)
where T(Pi) is the kinetic energy of the particle.
In its initial form, the Schrödinger equation for such a particle involved an object called an energy operator H, derived from the previous function, and giving rise to a differential equation for a function Ψ (Qi) called the wave function of which the square gives the probability of measuring the particle with the value Qi of its position.
The formulation of quantum mechanics makes use of all this and generalises it. We still have an energy operator H but the wave function is merely a special case of the state vector (think of thermodynamics) of any physical system.
To clearly show the departure from the concept of wave function this vector is denoted by Ι Ψ >. This is Dirac's vector notation for introducing Fourier analysis abstracted from Hilbert's functional analysis for linear partial differential equations.
An observable dynamic variable A, transcribed in the form of a linear operator A, can then have a series of values an during a measurement. Experience shows that there is a probability IcnI 2 of observing each value an, and that the state vector of the system is written as a vector sum of the base vectors associated with each value an such that:
Ι Ψ > = ∑ cn Ι an >
where
∑ ΙcnΙ 2=1 with n=1,2 ....
as required for introducing probabilities.
The base vectors Ι an > and the values an are called the eigenvectors and the eigenvalues of the linear operator A .
It is in this sense that we speak of a superposition of states in quantum mechanics. The coefficients cn are complex numbers of which the square gives the probability of finding the system in the state cn Ι an > of its dynamic variable A. This can be the position, the speed and quantum state variable that can be associated to express the characteristics of the system.
In the case of electrons, the phenomena of diffraction and interference which they display depend precisely on this principle of superposition of states applied to their states of position. Except that it is not a question of a series of discrete values xn for Q1=x=A1 but a continuous distribution. It is also for this reason that, generally speaking we refer to probability amplitudes for cn by analogy with light waves where the square of an amplitude gives the intensity of the light at a given point.
Schrödinger's equation in its general form is then an equation of change written:
(ih/2π) d Ι Ψ >/dt = H Ι Ψ >
If we have correctly understood the long arguments developed above we should not be surprised that as soon as we can define an energy and physical variables for any system, Schrödinger's equation above will apply and is absolutely not confined to notions of the change in space and time of a particle in a potential.
In particular, if the system were a quantum animal that could take the form either of a quantum whale or a quantum dolphin, in the sense where there would be two energy states for the same physical system, such as a quantum aquatic mammal, Schrödinger's equation would apply!
And this is what happens in neutrino or K meson oscillation phenomena, and also in the multiplets of isospin such as quarks and leptons in the electroweak theory and in QCD.
It is clear that this has nothing to do with notions of wave-corpuscle duality and wave mechanics.
During a measurement the state vector makes a quantum jump to now consist only of I an >. By analogy with a superposition of plane waves in a wave packet, we speak of reduction of the wave packet for the wave function of the position of a particle and, generally speaking, of reduction of the state vector for a quantum system.
With these fundamental notions in mind, we can study the phenomenon of entanglement in somewhat more detail.
Consider a simple quantum system, a quantum coin in a game of quantum heads or tails.
The base state vectors will be Ι f > and Ι p > for heads and tails. The coin can be in a state of quantum superposition such that its state vector is:
Ι Ψ > =c1 Ι f >+c2 Ι p >
where Ic2I2 will give the probability of observing the coin in the state of heads, for example.
If we use two coins A and B; we will then have two state vectors:
Ι ΨA > = c1a Ι fa >+c2a Ι pa > et Ι ΨB > =c1b Ι fb >+c2b Ι pb >
The two coins are considered as initially having no interactions, which means that we will have two independent Hamiltonians Ha and Hb.
Let H be the Hamiltonian of the system made up of these two coins and I psi > its state vector.
Then H =Ha+Hb and the state vector of the complete system and the most general form of the solution to the Schrödinger equation is a rather special product called a tensor product (χ) of the state vectors of each coin.
Thus
Ι Ψ > = ( c1a Ι fa >+c2a Ι pa > ) (χ) ( c1b Ι fb >+c2b Ι pb > )
= c1a c1b Ι fa > (χ) Ι fb >+c1a c2b Ι fa > (χ) Ι pb >+ c2a c1b Ι pa > (χ) Ι fb >+ c2a c2b Ι pa > (χ) Ι pb >
This is just the abstract re-transcription of the technique of separation of variables in a partial derivative equation.
If the Hamiltonian can no longer be broken down into a sum of Hamiltonians of coins with no interactions, during a brief instant when the coins might be electrically charged for example, the state vector of the system can no longer be described exactly as a tensor product of the state vectors of its parts with no interactions.
And this is exactly what we call the entangled state!
But this requires some important explanations. The state vector is always the sum of tensor products of the base states, heads or tails of a coin with no interaction, but the coefficients giving the amplitudes of the probabilities of finding the results of observations of the two coins can no longer be broken down into products of the amplitudes of the states of each coin before interaction, i.e. entanglement.
If the two entangled coins are separated and transported to opposite antipodes, a measurement on one will instantly affect the quantum state of the other. This means that the results of measurements on the second coin will no longer be independent of measurements made on the first one.
The EPR paradox and Bell's inequalities are essentially based on an analogous situation with physical systems formally giving rise to the same mathematical equations.
Here we see the full power of the abstract formulation of quantum theory, and above all the nature of quantum theory itself, in the sense that general principles are at work in a large variety of different physical systems and they result in mathematical equations that are largely independent of the form and of the physical system and of the physical variables of the system.
So that if we wish to analyse any given quantum phenomenon, the principles of quantum mechanics can be tested with the physical system and the type of dynamic variable that are the easiest to produce experimentally.
And indeed, the EPR paradox was initially formulated with variables of position and momentum for a pair of particles. But it keeps its essential meaning if we take the spin variables of a pair of particles, whether they be electrons or photons, for example. This is the reason why David Bohm proposed to test the paradox in this form, and this is what Alain Aspect did in 1982 with a pair of entangled polarised photons.
Latest
Fill out my online form.



