-
 Biocenosis
Biocenosis
-
 Micron
Micron
-
 Brunner Glands
Brunner Glands
-
 CME
CME
-
 Echolocation
Echolocation
-
 EES
EES
-
 Hedged farmland
Hedged farmland
-
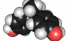 Endocrine disruptor
Endocrine disruptor
-
 Lagrangian point L2
Lagrangian point L2
-
 Denial of service
Denial of service
-
 Foreshore
Foreshore
-
 Sumoylation (SUMOylation)
Sumoylation (SUMOylation)
-
 Lipoglycan
Lipoglycan
-
 Excited state
Excited state
-
 Cephalopod
Cephalopod
-
 LH2
LH2
-
 Volcanism
Volcanism
-
 Linux
Linux
-
 Haemodynamics
Haemodynamics
-
 Turkey oak
Turkey oak
-
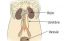 Pyelo-ureteric junction
Pyelo-ureteric junction
-
 Cholestasis
Cholestasis
-
 Cortisol
Cortisol
-
 Leukaemia
Leukaemia
-
 Amniotic fluid
Amniotic fluid
-
 Spermophilus
Spermophilus
-
 Semi hybrid
Semi hybrid
-
 Anisodactyl
Anisodactyl
-
 Plain text
Plain text
-
 Fischer-Tropsch process
Fischer-Tropsch process
Phase space
In analytical mechanics, the phase space is a space with 2M dimensions that can be used to give a geometrical interpretation of a mechanical system described by second order differential equations with respect to time. It is intimately related to the Hamilton equations and therefore to Hamiltonian formalism. The 2M dimensions correspond to the M pairs of conjugate variables involved in the differential equations governing the movement of a mechanical system (a simple example is given below).
This a fundamental space in physics and we find it at the heart of the formulation of quantum mechanics and statistical mechanics.
It was initially introduced into the problems of celestial mechanics to describe the mechanics equations of material points in a potential and the trajectories of light rays in non-homogeneous media with variable refractive indices in a unified manner; Schrödinger made use of it to construct wave mechanics from the ideas of De Broglie. Before this, Bohr and Sommerfeld had used it in quantum theory to express the quantification rules for simple mechanical systems.

Henri Poincaré (1854-1912)
Poincaré also made extensive use of this space to introduce geometrical reasoning into celestial mechanics and to study three-body problems. These studies were to form the basis of chaos theory.
In concrete terms, in the example of a gas made up of N particles, the phase space will be of 6N=2M dimensions. There will be 3N position coordinates and 3N momentum coordinates
. These are called generalised coordinates because they can correspond to different systems of cartesian, spherical, hyperbolic etc. coordinates.
More generally, the generalised coordinates and
represent conjugate variables of an arbitrary mechanical system. In the case of a gyroscope or a spinning top, these coordinates will be angles in the first case and kinetic motion in the second case.
The trajectory of a mechanical system is therefore represented by that of a point with 2M coordinates in the phase space. When considering the various initial conditions, there will be different curves in this space. This will allow a statistical mechanical study of the average behaviour of a set of identical mechanical systems in the form of a particle fluid. In chaos theory, phase space allows to see that the trajectories of non-linear systems with various initial conditions are sometimes close to certain geometrical forms in this space. This is referred to as a strange attractor, because everything takes place as if strange forces were attracting the points representing the mechanical system and forcing them to remain in their local region.

Trajectories in phase space represent the Lorenz strange attractor in 2D
Credit: Josep Sardanyés Cayuela
The geometrical theory of phase space involves group theory and allows mechanical theorems to be expressed in terms of geometrical theorems. This is called symplectic geometry and is involved in the geometrical formulations of quantum mechanics.
Phase space theory is not limited to discrete physical systems made up of a finite number of degrees of freedom. It can be generalised to be applied to field theory and this is what was done in general relativity and in the Yang-Mills field theory of elementary particles.
To find out more:
Latest
Fill out my online form.



