-
 Coconut
Coconut
-
 Toxoplasmosis
Toxoplasmosis
-
 Lemon
Lemon
-
 Active site
Active site
-
 Fast neutron reactor
Fast neutron reactor
-
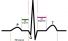 Electrocardiogram
Electrocardiogram
-
 Phases of the Moon
Phases of the Moon
-
 Crater
Crater
-
 Magnet
Magnet
-
 Taurids
Taurids
-
 Bunsen Burner
Bunsen Burner
-
 PCM
PCM
-
 DDT
DDT
-
 Dry ice
Dry ice
-
 Equinox equation
Equinox equation
-
 HDCP
HDCP
-
 Alar bar
Alar bar
-
 Work hardening
Work hardening
-
 Methanisation
Methanisation
-
 Scanner
Scanner
-
 Apricot
Apricot
-
 Hovering
Hovering
-
 Propellant
Propellant
-
 Amniocentesis
Amniocentesis
-
 Cosmological constant
Cosmological constant
-
 Zenith distance of a direction
Zenith distance of a direction
-
 Equatorial coordinates of a direction
Equatorial coordinates of a direction
-
 Caudal
Caudal
-
 Vigabatrin
Vigabatrin
-
 Organic agriculture
Organic agriculture
Loop quantum gravity
Loop quantum gravity is one of the main subjects of research on the problem of devising a theory capable of describing the quantum aspect of gravitation. A quantum theory of gravitation is needed to understand the birth of the universe and what happens inside black holes. In classical general relativity, in these situations there are singularities with undesirable divergences of certain physical quantities. The requirement for consistency in the laws of physics also demands the unification of the laws of quantum mechanics and the laws of space-time. This is why theoretical physicists have been searching for a mythical theory of quantum gravitation for decades.
The subject of quantum gravitation is extremely vast and it would probably take hundreds of pages to do it justice. It is well known that applying quantum mechanics to Einstein's equations of general relativity leads to infinite divergences when an attempt is made to couple the gravitation field to matter. There are situations in which approximate calculations of quantum gravity can be made without uncontrollable infinite quantities emerging. This is the case in some simple cosmology models described by what is called canonical quantum gravity and introduced in the 1960s by John Wheeler and above all Bryce DeWitt.
Quantum cosmology
To summarise, it is sought to apply the standard, so-called canonical, rules of quantification to Einstein's equations, meaning that an attempt is made to cast the latter in a so-called Hamiltonian form which is well known in analytical mechanics. To do this, like for the mechanics of a particle system, a phase space and a Hamiltonian function H must be introduced representing the total energy of the gravitational field+matter system. Just as a point in the phase space represents a set of possible positions-momentums for particles moving under the action of forces, a point in the phase space of the gravitational field will represent a possible state for the geometry of space-time curved by the presence of matter, and more generally of momentums and energies This space-time configuration space has been named superspace (not to be confused with supergravity).
A Schrödinger equation can then be constructed with a wave function the square of which gives the probability of finding the geometry of space-time in a given state. This is precisely the Wheeler-DeWitt equation. The problem is that, unlike with N particles, the geometry of space-time is described by a tensor field with 10 components defined at each point in space-time. As there are an infinity of these it is easy to understand that solving such an equation is not an easy task. However, if a class of possible geometries is first defined depending only on a small number of parameters certain calculations do become possible. This amounts to truncating the preceding phase space by "freezing" degrees of freedom so as to only keep a mini superspace.

On a sphere, transporting a vector tangent to a curve parallel to itself along a loop does not bring this vector back identically. Thus it can be seen that the orientations of a tangent vector transported parallel to the north pole along a path NBA and along a path NA differ by an angle α. On a plane surface, this angle would be zero. Considering a set of loops of this kind on a curved space-time ,knowing the results of calculations of parallel transports of vectors along these loops characterises the curvature and shape of space-time. It is the quantum treatment of these loops that is used to produce loop quantum gravity. © Luca Antonelli-wikipedia
The simplest case is when the consistent and isotropic Friedman-Robertson-Walker (FRW) models are taken with the simplest imaginable field as the origin of the gravitation field: a scalar field described by a Klein-Gordon equation with a potential V(
). The evolution over time of the gravitational field is here reduced to a single degree of freedom a(t). The Hamiltonian function of the system then takes a form similar to the one describing a particle with two position coordinates, here a(t) and
(t), moving in a complicated potential. The quantification rules of such a system are well known in wave mechanics and the quantum equation describing these simple models of the universe is not more but less complicated than those encountered in atomic or molecular physics.
The problem of the initial cosmological singularity
As was hinted at above, in classical general relativity, the FRW models are problematical, as are many others, because it can be shown that when t=0 the curvature of space-time becomes infinite. The very notion of space-time collapses, blocking everything. The beginning of the universe, if this notion has a meaning, is then completely out of the reach of human knowledge. Similarly, an identical situation occurs when a star collapses to give a black hole in classical general relativity a space-time singularity forms and the laws of physics are broken.
But this is not the first time that physics has been confronted with this type of problem. When the first models of atoms were being constructed, the electron rotating around the nucleus was in an unstable situation and ought to have ended up by collapsing into the nucleus and creating a singularity, there too, but not in space-time. The introduction of quantum mechanics and wave mechanics with a wave function, had then shown that there was only one series of discrete dynamic states accessible to the electron, the Bohr atom's famous energy levels. The wave function describing the probability of finding the electron in a region of space "spread" this very position making the previous collapse impossible.
John Wheeler and Bryce DeWitt had clearly indicated that a similar process should occur with their Schrödinger equation of space-time. The singularities in general relativity would therefore probably be "smoothed" by quantum processing thereby preventing their formation.
Results pointing to this had already been obtained in the late 1960s especially in the famous Hartle-Hawking model with imaginary time in the early 1980s. Unfortunately, as indicated above, each time it was the case of a very special situation in which the geometry of the universe was assumed not to depart very much from a certain form of consistency and isotropy that made it possible to considerably simplify the calculations. This is not satisfactory because such assumptions, though justifiable from certain aspects, are nevertheless wishful thinking. The theory should start from arbitrary space-time not partially predetermined and it is the calculations that should give the state of this space-time.
To do this the Wheeler-DeWitt equation would have to be solved in a general or generic manner, but how should this be done?
Ashtekar variables and loops
A considerable breakthrough was made in the mid 1980s. The Indian physicist Abhay Ashtekar, who had been a post-doctoral student of the great Roger Penrose, introduced a formulation of Einstein's equations in the phase space of space-time that considerably simplified their Hamiltonian formulation. What he showed was a situation that was formally very close to that obtained with the Yang-Mills equations, especially for QCD. The techniques from this gauge theory of strong nuclear reactions, quantum chromodynamics, could then be transposed.
It became apparent that the right variables to use were related to what are called holonomies, quantities that are calculated with parallel vector transports along loops in space-time.

The work of Carlo Rovelli led to the discovery that LQG predicted a discrete structure for space-time at around the Planck scale. © John Baez
Lacking a general solution to the Wheeler-DeWitt equation, Lee Smolin and Carlo Rovelli managed to find large classes of solutions to the Wheeler-DeWitt equation but above all, they managed to rigorously set out the solution space for this equation.
Like all Schrödinger equations, the solutions to these equations can be brought together in an abstract vector space similar to the usual space, this is the famous Hilbert space.
A solution is then described by a point in that space located by a "position vector" In the language of quantum mechanics, the wave functions corresponding to a particular space-time geometry are state vectors. The principle of the superposition of quantum mechanical states then implies that the geometry of space-time can be in the form of a superposition of states given by the vector sum of these vectors.
The most spectacular result was that it was possible, for the geometry of space-time, to construct surface and volume operators of which the spectra were discrete!
A discrete space-time for cosmology and the entropy of black holes
It is known that in quantum mechanics, quantities such as energy or momentum are given by operators. By acting on the wave function, which is mathematically similar to the function describing a light wave, the energy operator then extracts the various components of the spectrum of this wave. In the case of the hydrogen atom this gives discrete energy levels and orbits in which there is a discrete series of distances of the electron from the nucleus.
The situation is really very similar because Bohr's principle of correspondence also applies in the case of the spectrum of areas and volumes. As the quantum number of larger and larger orbits increases, the difference between the energy levels becomes smaller and smaller, as do the spatial distances separating the orbitals. The discrete spectrum becomes continuous and quantum physics merges into classical physics. Thus, for increasingly large volumes the classical notion of continuous space-time reappears.
Martin Bolowald was one of the first to see the implications in cosmology of the discrete character of space-time on the Planck scale given by LQG equations. He applied these to the previous FRW models and discovered several things.
Even within the approximation of mini superspace, the situation is much more under control because the fact that the geometry of space-time is discrete already considerably reduces the number of degrees of freedom possible for space-time on approaching the primordial singularity. This allows to better justify the use of mini superspaces because of the very structure of LQG.
It then appears that a curvature operator for space-time and an operator for "position" a(t) can be defined for the factor describing the expansion of the universe of FRW. Unlike the result obtained with LQG, the spectrum of these operators is discrete.
Amazingly, whereas the spectrum of the latter operator has a value 0 corresponding to zero volume, the curvature has a maximum bound, and the space-time singularity is eliminated!
There is then no problem in extending the structure of space-time to before what for us corresponds to time 0. There is then a "before the Big Bang". If the expansion factor of the universe with time is represented, it performs a movement reminiscent of a ball eternally bouncing elastically. This type of theory is called "bouncing Universe". It could be thought that each expansion-contraction reproduces an identical universe each time, but Bojowald pointed out that these quantum equations make the parameters describing each new cycle indeterminate, each time resulting in a loss of some of the information about the previous state.
The discrete nature of the areas in LQG has also been used to find out the relationship between the entropy of a black hole and the value of the area of the horizon of the black hole. This value had been obtained previously using string theory for some supersymmetric black holes. In LQG the result is, however, valid for a Schwarzschild black hole of the type known to exist in nature.
 One of the creators of loop quantum gravity, the theoretical physicist Abhay Ashtekar. © Kavli Institute
One of the creators of loop quantum gravity, the theoretical physicist Abhay Ashtekar. © Kavli Institute
Latest
Fill out my online form.



