-
 nEUROn technology demonstrator
nEUROn technology demonstrator
-
 Aplite
Aplite
-
 Conservation
Conservation
-
 Ecosystem
Ecosystem
-
 Parenteral
Parenteral
-
 Paragenesis
Paragenesis
-
 CNO Cycle
CNO Cycle
-
 MediaFLO
MediaFLO
-
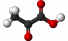 Pyruvate
Pyruvate
-
 Virtual memory
Virtual memory
-
 Polyphenol
Polyphenol
-
 Koua river prawn
Koua river prawn
-
 Carbon footprint
Carbon footprint
-
 Configuration
Configuration
-
 SQL
SQL
-
 FSB
FSB
-
 NIAID
NIAID
-
 Blob
Blob
-
 Venus Express
Venus Express
-
 Celestial equator
Celestial equator
-
 Plutoid
Plutoid
-
 Viking 2
Viking 2
-
 Melanocyte
Melanocyte
-
 Noma
Noma
-
 Mineral
Mineral
-
 The Darvaza gateway to hell
The Darvaza gateway to hell
-
 Epigenesis
Epigenesis
-
 Hydrothermal deposit
Hydrothermal deposit
-
 Sweet Chestnut
Sweet Chestnut
-
 Droid
Droid
Heisenberg inequalities
The inappropriately named Heisenberg uncertainty principle is today more correctly called the Heisenberg inequalities. These inequalities, listed in 1927 by the German physicist Karl Werner Heisenberg, indicate the limits of the relevance of using wave and classical particles concepts to describe phenomena on an atomic scale, such as those involving electrons and light.
They are incorrectly referred to as uncertainty relations or indeterminacy.
The three Heisenberg inequalities:
i varying from 1 to 3 to express x,y,z
= square root of the mean quadratic deviation on the position measurement
= square root of the mean quadratic deviation on the momentum
= Planck constant divided by
In no case do they indicate any imprecision or limit to the simultaneous knowledge of the position and momentum of a particle in the classical sense. They do not reflect a limit to knowledge but a limit to the application of the classical concepts describing mechanical phenomena at the atomic scale.
If we continue to describe matter and light in terms of particles and waves, we can only do so by having these concepts limit each other and by stating the probabilities of observing such and such a classical value of a classical object. The state vector of a particle in space then takes the form of a wave function giving the probability of observing the particle aspect of a quantum of energy at a point in space, using classical instruments.
There is then a calculation using mean values and mean quadratic deviations, but there is no question of probabilistic methods being used to describe a classical system, or more precisely a population of systems, for which certain information determining the state would be lacking, as is the case in the kinetic theory of gases.
It is in fact a general reformulation of the character and the way that a physical value observable in the universe changes.
If a state function for the two values A and B is considered, which may have nothing to do with a wave or particle image, then if these values are brought into a system having an energy function H in the Hamiltonian wave and particle theory, they will verify a Heisenberg inequality.
Thus we will be able to have an electric field E and a magnetic field B, energy E and time t, angular momentum J and an angle, etc.
Latest
Fill out my online form.



