-
 DVD audio
DVD audio
-
 Cryptochrome
Cryptochrome
-
 Spectral colour
Spectral colour
-
 Launcher Integration Building
Launcher Integration Building
-
 Whirlpool galaxy
Whirlpool galaxy
-
 Yellow dwarf
Yellow dwarf
-
 Watt
Watt
-
 Roaming
Roaming
-
 Amylase
Amylase
-
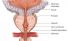 Prostate
Prostate
-
 Orbit
Orbit
-
 NAT
NAT
-
 Acceleration of the expansion of the universe
Acceleration of the expansion of the universe
-
 Spinplasmonics
Spinplasmonics
-
 Mineralogical class
Mineralogical class
-
 Hadal zone
Hadal zone
-
 Exhalation
Exhalation
-
 Arend-Roland comet
Arend-Roland comet
-
 Hox gene
Hox gene
-
 Ring Nebula
Ring Nebula
-
 Blood
Blood
-
 Massive Compact Halo Objects
Massive Compact Halo Objects
-
 Keplerian elliptic motion
Keplerian elliptic motion
-
 Virus
Virus
-
 Pelvis
Pelvis
-
 Antiemetic
Antiemetic
-
 Deoxyribose
Deoxyribose
-
 Opt-out
Opt-out
-
 Replicase
Replicase
-
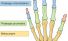 Phalanx
Phalanx
Hamiltonian
The notion of Hamiltonian, or Hamiltonian function, comes from a very powerful formulation of the equations of analytical mechanics, the Hamilton equations. These are fundamental in their general role in physics and are the basis of the discovery of the formulation of quantum mechanics.

Sir William Rowan Hamilton (1805-1865).
These equations were initially limited to mechanical systems having a finite number of degrees of freedom, such as the positions and velocities of particles in a gas, or the angles and rotation speeds describing a gyroscope; they can now be extended to describe continuous systems with an infinite number of degrees of freedom. This is the case with the equations of an electromagnetic or gravitational field, which can be cast in the so-called Hamiltonian form.
A simple example is enough to understand the meaning of these equations.
Consider a set of N particles in a gas which will then have 3N position coordinates and 3N velocity coordinates
where the dot denotes the total derivative of the preceding coordinate with respect to time, i.e.
.
We know that in the Lagrange formulation of the equations of the mechanics of a particle system, the differential equations of movement of these particles are given by:
Where the so-called Lagrangian function for these particles in a potential V is written
The masses are obviously the same for a particle and its three position coordinates. The first term on the right of the equation is a sum of kinetic energies.

Joseph Louis Lagrange (25 January 1736, Turin - 10 April 1813, Paris)
The Lagrangian formulation is invariant to a change in the coordinates of the system which is what makes it so powerful as it allows us to reduce large classes of differential equations expressed in Cartesian, spherical etc. coordinates to a few fundamental cases that we know how to solve.
Furthermore, it can be used to prove that the theorems of conservation of energy, momentum etc. are automatically valid for these large classes of differential equations since, by proving conservation laws in a given coordinate system we can be sure that they will be valid in other coordinate systems or for other mechanical systems that can be cast into equations in Lagrangian form.
The validity of the laws of conservation such as for energy or momentum, initially established for material points, will also be valid for electromagnetic fields if the Maxwell equations can be cast in Lagrangian form. And indeed they can.
The implications are actually very far reaching and have repercussions in quantum mechanics and in quantum field theory through Noether's theorem linking the invariance of the Lagrangian to certain symmetry transformations and the establishment of conservation laws.
Thus, if a differential equation is written with variables that have no direct relationship with the positions of a particle system, but deriving from a Lagrangian that can take the form of a particle system invariant to translation in time, then a function can be defined that corresponds to an energy and that will satisfy a conservation law.
The Lagrange formulation can be extended as follows. Another variable is introduced defined by
. A function can then be constructed called a Hamiltonian
, deduced from the previous Lagrangian by the Legendre transformation:
The system of Lagrangian second order differential equations can then be written in the form of a system of first order differential equations:
These are the Hamilton equations and they were to be of capital importance in the hands of Heisenberg, Born, Jordan and Dirac for the discovery and the formulation of matrix mechanics and its final extension, quantum mechanics. These physicists discovered that the transition from classical mechanics to quantum mechanics can be made by replacing the above quantities by matrices.
Here again of course, the Hamiltonian function expresses the total energy of the mechanical system being considered.
Several important consequences arise from these equations, which are also the basis of Gibbs's, Bolztmann's and Einstein's statistical mechanical formulation.
For example, these equations reduce the movement of N material points (particles of a gas, stars in a galaxy, etc.) to a single abstract point in a 6N dimension space of the Hamiltonian mechanical system called the phase space. The coordinates of this point are defined by 3N pairs of coordinates called conjugate coordinates et
.
These same equations are invariant to a large class of coordinate changes called canonical transformations of the previous conjugate variables. They are written:
This gives rise to a powerful integration technique for the equations of motion for a mechanical system as was initially demonstrated in celestial mechanics. This is why Bohr, and especially Sommerfeld, used it to study and construct atomic models with orbits of electrons around the nucleus of an atom.
Finally, there is a function that is highly important in Hamiltonian mechanics because it links the Hamilton and Lagrange formalisms.
This is the Hamilton-Jacobi equation.

Carl Gustav Jacobi (1804 - 1851)
The Lagrange equations can be differentiated starting from the condition that the function
is an extremum for all variations (in a precise direction) of the coordinates of positions and velocities of a mechanical system having a Lagrangian, between two dates separating the states of motion of the mechanical system being considered.
This function is called the action and it makes it possible to write the following equations:
The first one is the Hamilton-Jacobi equation itself and is related to the integration of the previous Hamilton equations.
It is this equation that allowed Schrödinger to develop wave mechanics.
The Hamilton function then became a linear hermitian acting on a function space, the Hilbert space of quantum mechanics. The so-called Hamiltonian operator is obtained from the expression for the total energy of a physical system, such as that of the hydrogen atom, of an electromagnetic field in a box, or even, as in the case of loop quantum gravitation, of the universe and its gravitational field coupled with matter.
To find out more:
Latest
Fill out my online form.



