-
 Dorsal
Dorsal
-
 API
API
-
 Astroparticle
Astroparticle
-
 Local ring network
Local ring network
-
 Red panda
Red panda
-
 Mysticeti
Mysticeti
-
 Hydrogen reaction engine
Hydrogen reaction engine
-
 antiacne
antiacne
-
 Crystal texture
Crystal texture
-
 Chorea
Chorea
-
 Radioactivity
Radioactivity
-
 Systematic
Systematic
-
 Basiphilous
Basiphilous
-
 Coal
Coal
-
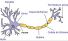 Dendrite
Dendrite
-
 Ecological footprint
Ecological footprint
-
 Anti-inflammatory
Anti-inflammatory
-
 Contraception
Contraception
-
 Fibroadenoma
Fibroadenoma
-
 Chiropraxis
Chiropraxis
-
 Redshift
Redshift
-
 MPLS
MPLS
-
 Codec
Codec
-
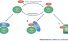 Sumoylation (SUMOylation)
Sumoylation (SUMOylation)
-
 Jerusalem artichoke
Jerusalem artichoke
-
 Propagule
Propagule
-
 Tomia
Tomia
-
 Anseriformes
Anseriformes
-
 Hydrogen vehicle
Hydrogen vehicle
-
 Orbiter
Orbiter
Correspondence principle
The Bohr correspondence principle states that at the limit of large quantum numbers for atomic systems the formulae of classical physics should be found. This principle has especially made it possible to connect the formulae giving the radiation intensities of quantum atoms to classical formulae. Therefore it has guided theoreticians toward an interpretation of quantum equations by connecting them to their classical limits.
More generally, the principle of correspondence in quantum mechanics gives the rules for constructing quantum equations from classical equations.
Thus, starting from the formalism of Hamilton analytical mechanics, with for example the Hamiltonian function H of N particles in a potential V:
where and
are the generalised coordinates of position and momentum, we know that the equations of motion for the system will be given by the following Hamilton equations:
the dot denotes a derivative with respect to time.
Furthermore, for functions of generalised coordinates such as , there will respectively be the Poisson brackets:
and the Poisson equations:
The correspondence rules stipulate that the observable values must be replaced by linear Hermitian operators in the previous equations to obtain the quantum equations.
Thus the Poisson brackets will become
where
In particular for a value with a Hamiltonian operator
, the following Heisenberg equation is obtained:
Finally, the Hamilton-Jacobi equation
will be transformed into the Schrödinger equation for N particles in a potential with the Hamiltonian operator
And
where is a wave function in the configuration space for N particles.
Latest
Fill out my online form.



