Graph theory

A graph is a collection of elements in a system of inter-relations. Geometrically, these elements are represented by points (vertices) interconnected by the arcs of a curve (the edges). According to whether we choose to direct the edges or to give them a weight (a cost of passage); we speak of directed graphs or weighted graphs.

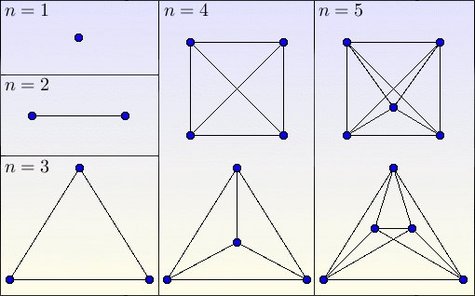
Complete graphs are those where all the vertices are connected pairwise.
Credits: S. Tummarello

The theory of graphs is concerned with their multiple properties: the existence of the shortest or cheapest routes, of particular cycles (Eulerian, Hamiltonian etc.), the number of intersections in the plane, colouring problems, etc.

The graph K_3,3 is not planar: the edges intersect at at least one point in the plane.
Credits: S. Tummarello

Graph theory goes back to the problem of the bridges of Königsberg: is it possible to walk through this town via a circuit that passes once and only once over each of the seven bridges? In modern terms, the problem is to show the existence of a Eulerian cycle in the associated graph: In 1736, Euler showed that such a route did not exist.

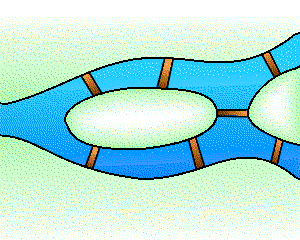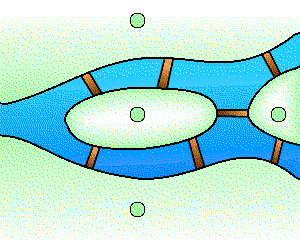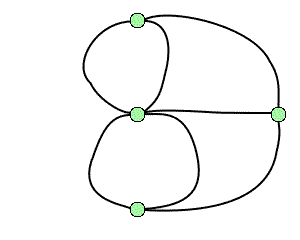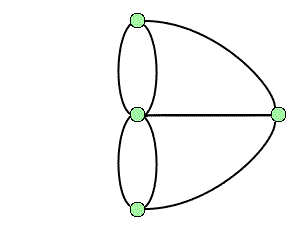
The graph associated with the problem of the bridges of Königsberg.
Credits: S. Tummarello

Today, graphs have very many applications in modelling networks (roads, information, etc.). Moreover, graph theory has brought up algorithm problems (the travelling salesman problem, graph colouring, calculation of the largest sub-graph common to two graphs etc.), which are crucial in complexity theory (NP-complete problems, the P=NP conjecture).